Logic: Create a pivot element & arrange elements with two partitions, If the elements are lesser than pivot add it to left partition & if elements bigger than the pivot arrange it to right side of partition & make call recursively with the subarray found with same approach.
Time Complexity: Avg O(n^2) .. Best: O(n log (n))
Space Complexity: O(n)
Worst case Time complexity of QuickSort is O(n^2) Let say we have sorted array & we applied Quick sort so the recursion will go as — n , n-1, n-2, n-3….. Which is sum of arithmetic number which is n(n+1)/2 = O(n^2)
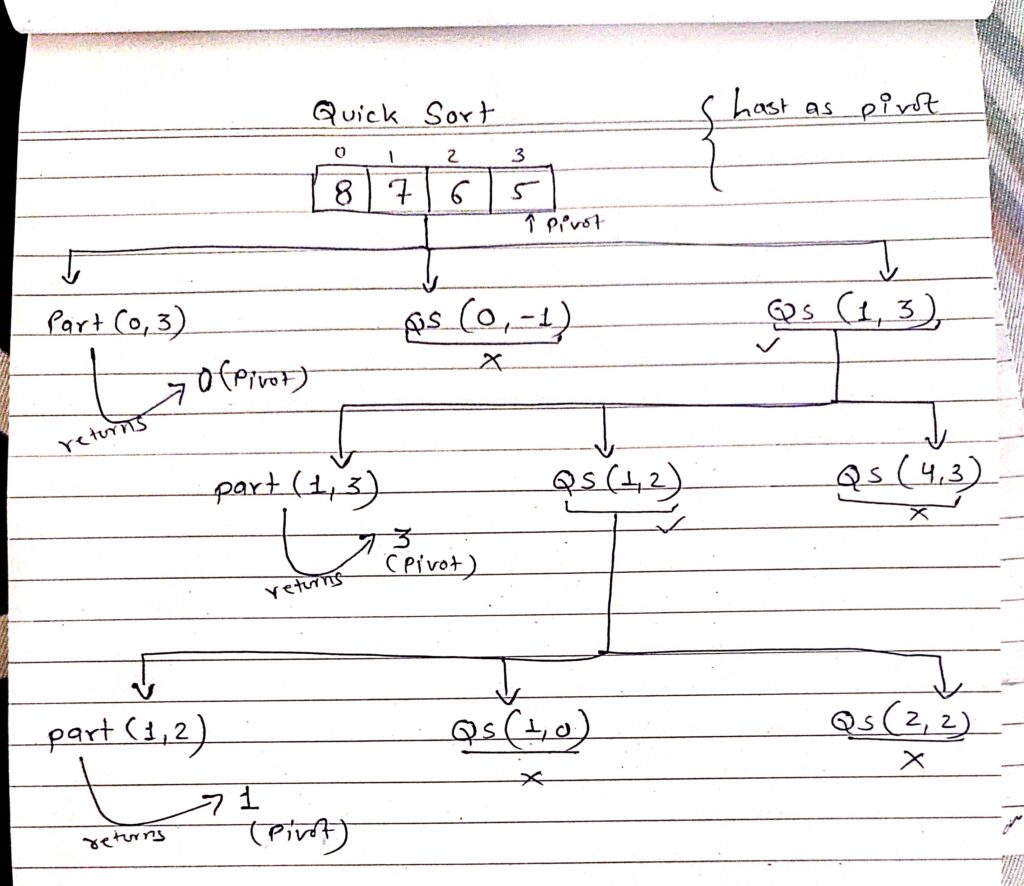
//Approach #1 create pivot element & sort elements which are lesser than the pivot to right & bigger on left.
// Here we are taking pivot as last element...
func quickSort(_ arr: inout [Int], _ lowerBound: Int, _ upperBound: Int) {
if lowerBound < upperBound {
let pivot = partition(&arr, lowerBound, upperBound)
// print("pivot is-->", pivot)
quickSort(&arr, lowerBound, pivot-1)
quickSort(&arr, pivot+1, upperBound)
}
}
func partition(_ arr: inout [Int], _ lowerBound: Int, _ upperBound: Int) -> Int {
// print("part-- lower, upper---->", lowerBound, upperBound)
let pivot = arr[upperBound] // pivot
var i = (lowerBound - 1) // Index of smaller element and indicates the right position of pivot found so far
for j in lowerBound..<upperBound {
// If current element is smaller than the pivot
if arr[j] < pivot {
i+=1 // increment index of smaller element
arr.swapAt(i, j)
}
}
i+=1
arr.swapAt(i,upperBound)// Placing the pivot at right position so xx(lesser elements) Pivot xx(larger elements)
return i
}
var arr = [8, 7, 6, 5]
quickSort(&arr, 0, arr.count - 1)
print("Quick Sort-->", arr)