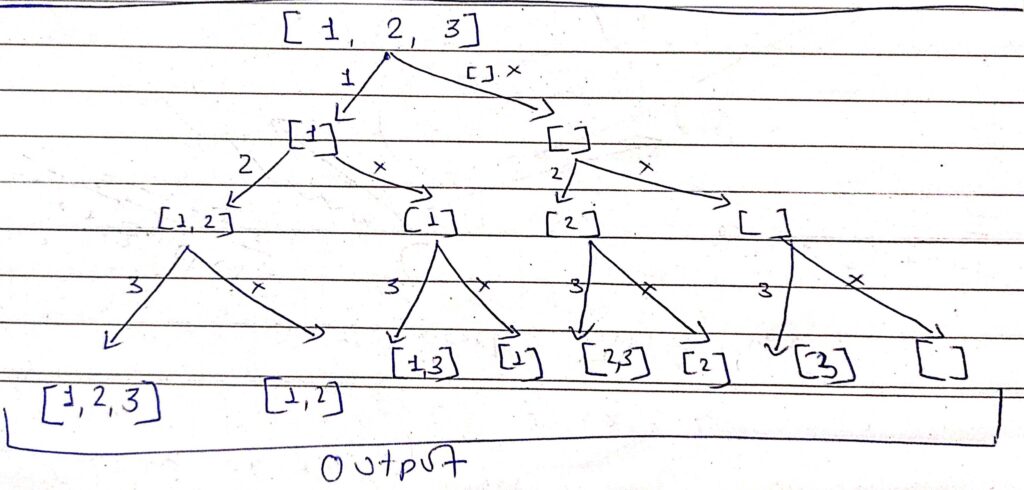
[Question]: Given an integer array that may contain duplicates, find all possible subsets (the power set). No duplicates allowed in answer. Solution in any order allowed.
Input: nums = [1,2,3] Output: [1,2,3] [1,2] [1,3] [1] [2,3] [2] [3] []
class Solution {
func subsetsWithDup(_ nums: [Int]) -> [[Int]] {
guard nums.count > 0 else { return [] }
var output = [[Int]]()
var candidates = [Int]()
let startIndex = 0
let sorted = nums.sorted()
uniqueSet(&output, &candidates, startIndex, sorted)
return output
}
// This is kind of simillar to the "inorder traversal"
private func uniqueSet(_ output: inout [[Int]], _ candidates: inout [Int], _ startIndex: Int, _ nums: [Int]) {
//Entering valid values store each case("node")'s value
output.append(candidates)
// try to find if it has "children", if no "child", we done
for i in startIndex..<nums.count {
// filter out cases which may cause duplicate subsets
guard i == startIndex || nums[i] != nums[i - 1] else { continue }
// update candidates to next level's value(child's value)
candidates.append(nums[i])
// startIndex + 1, go next level(go to its child)
uniqueSet(&output, &candidates, i+1, nums)
// update candidates to previous level's value(parent's value)
candidates.removeLast()
}
}
}
// ex: [1, 2, 2]; assume it is like a tree(inorder traversal), "*" indicates duplicated case
// []
// / \ \
// [1] [2] [*2]
// / \ |
// [1, 2] [1, *2] [2, 2]
// /
// [1, 2, 2]
// output: [[], [1], [1, 2], [1, 2, 2], [2], [2, 2]]Approach #2: Using Bitwise Operator
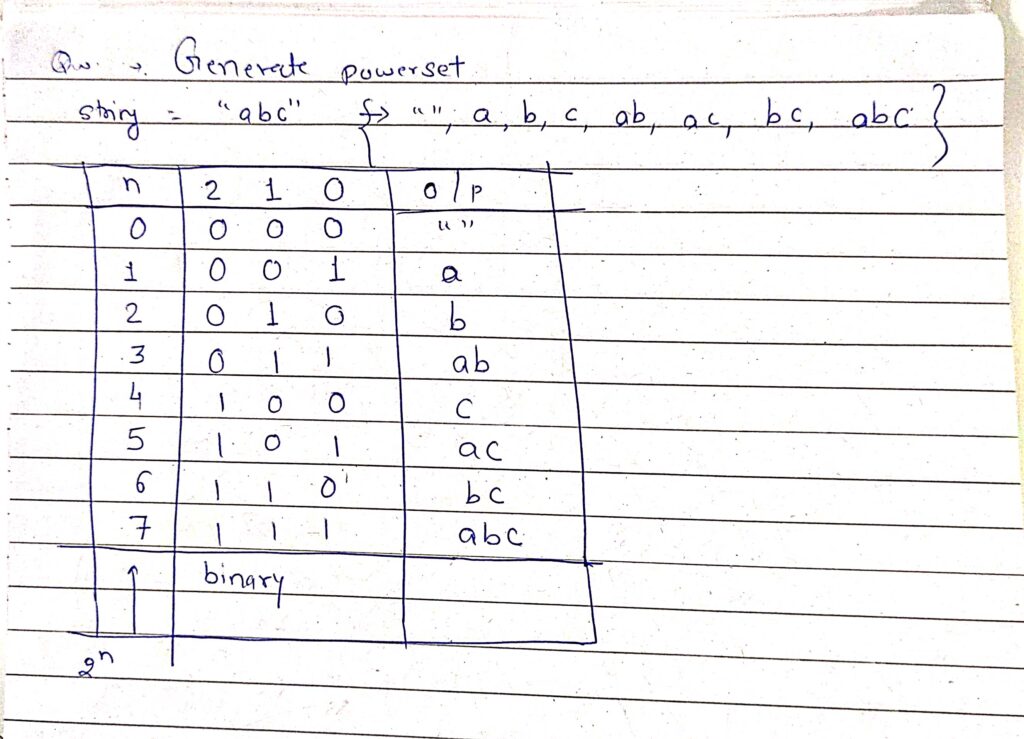
Question: Power Set: Print all the possible subsequences of the String
To check whether the ith bit is set or not.If n&(1<<i) != 0,then the i-th bit is set.
First, write down all the numbers from 0 to 2^(n)-1 and their bit representation.
0 -> no-pick , and 1-pick
// TC: (2^n X n) FirstLoop X Second Loop
// SC: O(n)// for saving output
func generateAllSequence(input: String) -> [String]{
var n = input.count
var output:[String] = []
for num in 0..<(1 << n) {
var sub = "";
for i in 0..<n {
if (num & (1 << i)) != 0 {//check if the ith bit is set or not
let index = input.index(input.startIndex, offsetBy: i)
sub += String(input[index])
}
}
if !sub.isEmpty {
output.append(sub);
}
}
return output;
}
let subSet = generateAllSequence(input: "abc")
print("generateAllSequence using BitOperator--->", subSet)
// ["a", "b", "ab", "c", "ac", "bc", "abc"]